Los retos resueltos en este writeup pertenecen a un CTF presencial celebrado el pasado 10 de Noviembre en las jornadas de ciberseguridad de CIBER.gal.
Crypto
Descodificando
¡Vaya! me han pasado esta cadena de caracteres, pero no sé qué significa. ¿Puedes ayudarme a descifrarla?
En este reto se nos proporciona un fichero con los siguientes contenidos. Estos estan codificados en BCD por lo que podemos usar una herramienta online como Cyberchef para realizar la conversión.
00110011 00110010 00100000 00110110 00110101 00100000 00110110 01100101 00100000 00110101 00110100 00100000 00110110 00110100 00100000 00110011 00110000 00100000 00110101 00110101 00100000 00110100 00110010 00100000 00110100 01100100 00100000 00110111 00110011 00100000 00110101 00110101 00100000 00110110 00111000 00100000 00110011 00110011 00100000 00110100 01100011 00100000 00110100 00110100 00100000 00110110 00110001 00100000 00110100 00111000 00100000 00110011 00111000 00100000 00110111 00110111 00100000 00110011 00111001 00100000 00110011 00110110 00100000 00110111 00111000 00100000 00110110 00111001 00100000 00110110 01100001 00100000 00110100 00110101 00100000 00110100 01100101 00100000 00110110 00111001 00100000 00110110 00111001 00100000 00110011 00110011 00100000 00110111 00110111 00100000 00110011 00111000 00100000 00110100 00110100 00100000 00110111 00111000 00100000 00110101 00110111 00100000 00110100 00110011 00100000 00110100 00110011 00100000 00110111 01100001 00100000 00110100 00110111 00100000 00110110 00110111 00100000 00110011 00110111 00100000 00110011 00110010 00100000 00110110 00110101 00100000 00110110 00110010 00100000 00110011 00110100 00100000 00110100 01100110 00100000 00110011 00110110 00100000 00110011 00110010 00100000 00110111 00110111 00100000 00110111 00110110 00100000 00110100 00110001 00100000 00110100 00110100 00100000 00110011 00110111 00100000 00110100 00111001 00100000 00110100 01100110 00100000 00110011 00110111 00100000 00110110 00110101 00100000 00110101 00110111 00100000 00110110 00111000 00100000 00110111 00111000 00100000 00110011 00111001 00100000 00110111 00111000 00100000 00110011 00110001 00100000 00110100 00110100 00100000 00110101 00110000 00100000 00110111 00110000
Al transformarlo de BCD a ASCII obtenemos el siguiente texto. Este está en hexadecimal, por lo que podemos usar de nuevo esta herramienta anterior.
32 65 6e 54 64 30 55 42 4d 73 55 68 33 4c 44 61 48 38 77 39 36 78 69 6a 45 4e 69 69 33 77 38 44 78 57 43 43 7a 47 67 37 32 65 62 34 4f 36 32 77 76 41 44 37 49 4f 37 65 57 68 78 39 78 31 44 50 70
El texto que se obtiene después es el siguiente, el cual está en formato base62.
2enTd0UBMsUh3LDaH8w96xijENii3w8DxWCCzGg72eb4O62wvAD7IO7eWhx9x1DPp
Tras decodificarlo de base62 podemos observar que la salida es una cadena en base64.
Y2liZXJnYWx7SGFzX2Rlc2NvZGlmaWNhZG9fbGFfZmxhZ30=
Finalmente descodificándolo de base64 conseguimos la flag.
cibergal{Has_descodificado_la_flag}
RSA Madness
Alberto, el hermano pequeño de Alicia, ha creado dos claves RSA 1024 por miedo a extraviar una de ellas. Aunque su hermana se lo ha desaconsejado, a Alberto le ha parecido una gran idea que ambas claves compartan el mismo módulo (n), como se puede observar analizando sus respectivas claves públicas: pub_key1.pem y pub_key2.pem
Bernardo ha enviado un mensaje cifrado a Alberto, utilizando aes-256-cbc, con el vector de inicialización (IV) a 0, y ha cifrado la clave AES de 256 bits con la primera clave pública RSA de Alberto. En tu puesto de vigilancia has obtenido el mensaje cifrado con AES (flag.enc) y la clave AES cifrada (aes_key.enc1).
Como era previsible, Alberto ha extraviado la clave privada asociada a su primera clave RSA, por lo que solicita a Bernardo que le remita de nuevo la clave AES cifrada con su segunda clave pública RSA, información que también has obtenido (aes_key.enc2).
¿Serás capaz de descifrar la clave AES y acceder al mensaje cifrado?
En este reto se nos proporcionan 4 ficheros:
pub_key1.pempub_key2.pemaes_key.enc1aes_key.enc2flag.enc
Si analizamos las claves públicas podemos comprobar que tal y como se nos dijo en el enunciado, ambas tienen el mismo módulo (n) pero distinto exponente (e). Ya que comparten módulo y tanto el fichero aes_key.enc1 como aes_key.enc2 son el mismo mensaje (pero cifrado con una clave pública distinta) este reto se puede resolver gracias al ataque del módulo común.
Ataque
Para que el ataque del módulo común funcione, los exponentes de cada clave deben de ser coprimos entre si, es decir, $mcd(e_1, e_2)=1$. Si es así, significa que tenemos dos números $x$ e $y$ tal que: $$xe_1 + ye_2 = 1$$ Para calcular $x$ e $y$ utilizamos el algoritmo de euclides extendido. Una vez calculados, teniendo en cuenta que $C_1=M^{e_1} \bmod n$ y que $C_2=M^{e_2} \bmod n$ :
$$ \begin{aligned} C^x_1 * C^y_2 &= (M^{e_1})^x * (M^{e_2})^y \newline &= M^{e_1x} * M^{e_2y} \newline &= M^{e_1x + e_2y} \newline &= M^1 \newline &= M \end{aligned} $$
Resolución del reto
Para resolver este reto podríamos pasar lo descrito anteriormente a código, pero ya existe en github un script en python que se puede utilizar precisamente para esto. RSA-Common-Modulus-Attack.
Para obtener la clave con la que se cifró la flag, simplemente ejecutamos el script de la siguiente manera:
# enc1 y enc2 son los ficheros de aes en base64
rsa-cm.py -c1 enc1 -c2 enc2 -k1 pub_key1.pem -k2 pub_key2.pem
Con ello obtenemos el siguiente resultado:
[+] Recovered message:
30593212847270711399711376013419410780738043650221125144037099091540978173011
[+] Recovered bytes:
b'C\xa3%\x14\x9f\xb5C\xa2"tb\x9e\xf6\xbf\xd3l\xb0\xb6Lpg\x8c\nO\x02\xd7x\xb0\x14\xb4\x04S'
Esta es la clave utilizada para cifrar el fichero flag.enc con AES, por lo que solamente nos queda descifrar. Una manera fácil de hacerlo, es pasar la clave obtenida y el fichero flag.enc a hexadecimal, y utilizar una herramienta online como Cryptii para obtener el mensaje descifrado.
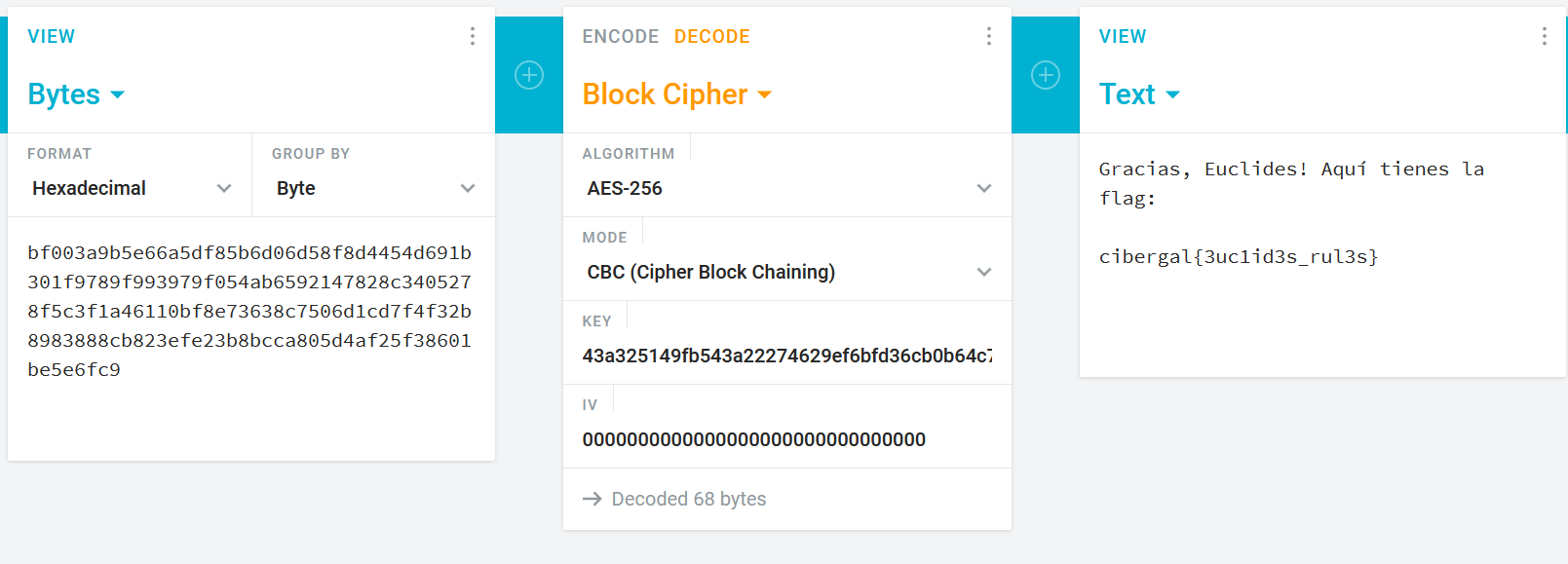
Flag:
cibergal{3uc1id3s_rul3s}
RSA Madness 2
De nuevo Alberto, el hermano pequeño de Alicia, ha creado un servicio web (https://cibergalctf-rsa-madness-2.chals.io) que devuelve firmado con su primera clave RSA el número que se proporcione. Desoyendo de nuevo los consejos de su hermana, ha utilizado esa clave para recibir información confidencial. Bernardo ha enviado a Alberto cifrado con la clave pública RSA (pub_key1.pem) un mensaje que has podido interceptar (flag2.enc)
Para este reto se nos proporcionan 2 ficheros:
pub_key1.pemflag2.enc
Y se nos proporciona una url de un servicio web en el que nos firman cualquier número proporcionado con la clave privada asociada a la clave pública con la que fue cifrada la flag.
El hecho de utilizar en este servicio de firmas el mismo par de claves que se utilizó para cifrar, es un fallo de seguridad importante. Un atacante podría proporcionar un mensaje que fue cifrado con la pública a la aplicación de firma y obtener la versión en texto plano de este.
En la siguiente tabla se muestran como son los procesos de cifrado, descifrado y firma.
| Cifrado | Descifrado | Firma |
|---|---|---|
| $C=m^e \bmod n$ | $m=C^d \bmod n$ | $S=m^d \bmod n$ |
Como se puede observar, si al proceso de firma se le proporcionara como mensaje a firmar un texto cifrado con la clave pública ($e$ y $n$) con la que se realiza la firma, se podria descifrar el mensaje.
Sin embargo, cuando introducimos en la aplicación web el mensaje cifrado (es decir, flag2.enc pasado a integer), se nos devuelve el siguiente mensaje.

Esto se debe a que la aplicación web no permite la firma de ese mensaje ya que quien la programó sabe que fue cifrado con la clave pública asociada a la clave con la que se firma.
Por lo tanto tenemos que encontrar una manera de que la aplicación firme el mensaje cifrado pero sin saber que es el mensaje en cuestión. Para ello utilizamos un método conocido como firma a ciegas.
Firma a ciegas
La firma a ciegas se utiliza cuando, por privacidad o anonimato, un usuario quiere que un mensaje sea firmado sin que la persona que firma conozca el contenido del mismo.
Este método funciona de la siguiente manera. Escogemos un valor $k$, el cual ha de ser coprimo con $n$. Siendo $n$ el módulo y $e$ el exponente público, ofuscamos el mensaje de la siguiente manera.
$$m' \equiv mk^e \bmod n$$
A continuación, enviamos el mensaje ofuscado $m'$ para ser firmado.
$$S' \equiv (m')^d \bmod n \equiv (m^ek^e)^d \bmod n$$
Por último, para obtener el mensaje desofuscado simplemente tendríamos que dividir por $k$. Teniendo en cuenta que uno de los factores que conforman $m'$ es $k^{ed}$ , al dividir por $k$ quedaría $1^{ed}$ que es $1$.
$$S = \frac{S'}{k} \bmod n$$
Resolución del reto
Ahora que sabemos como funciona el método de firma a ciegas, lo vamos a aplicar en nuestro reto.
En primer lugar, tenemos que pasar el fichero flag.enc a integer. Su valor es el siguiente:
m = 136303048756995810157940716185032667111830612010597107406495676976962913830094230393545978589443439249697298402573338272253640904169975859184422021013590534948130017584626517376422117912593883984359625006567897844040686762271735646197621493539236449652734497036337238540068933149508980465458044755934584078886
En segundo lugar, debemos extaer del fichero pub_key1.pem los factores $e$ y $n$.
e = 65537
n = 154087653999555555446998804473067505160067050493140267558659897792940250300855911633655658601345747714095446260307217652438694220001628702699560693661391270787633897136259675951607773082816805013014361131686525312985034121386722108595596708517831422886817991765720117085738934471183106649399960872754505418483
A continuación, seleccionamos un número que sea coprimo con n. En nuestro caso, seleccionamos el 2.
Ahora realizamos el proceso de ofuscación del mensaje cifrado. Para realizar el cálculo, podemos usar ipython por ejemplo.
m1 = m*(k**e) % n
Enviamos este número para ser firmado por la aplicación web y obtenemos el siguiente número.
s1 = 7849746955854748602350158963065991715871888549798095025878829707724270519846341645847019231536931761434479614627261827551978821373938357638164
Por último, para la obtención de la flag, solamente tenemos que dividir este resultado entre $k$, es decir, entre 2. Y tras esa división, pasar el resultado a bytes.
from Crypto.Util.number import long_to_bytes
k = 2
s1 = 7849746955854748602350158963065991715871888549798095025878829707724270519846341645847019231536931761434479614627261827551978821373938357638164
a = long_to_bytes(s1 // k)
print(a.decode('utf-8'))
Flag:
Resuelto usando firma ciega!!
cibergal{RSA_love_is_blind}