The challenges from this writeup are from an in person CTF that took place last November 10th at CIBER.gal’s cibersecurity conferences.
Crypto
Descodificando
¡Vaya! me han pasado esta cadena de caracteres, pero no sé qué significa. ¿Puedes ayudarme a descifrarla?
On this challenge we are given a file with the following content. Since they are BCD encoded, we can use an online tool such as Cyberchef to decode it.
00110011 00110010 00100000 00110110 00110101 00100000 00110110 01100101 00100000 00110101 00110100 00100000 00110110 00110100 00100000 00110011 00110000 00100000 00110101 00110101 00100000 00110100 00110010 00100000 00110100 01100100 00100000 00110111 00110011 00100000 00110101 00110101 00100000 00110110 00111000 00100000 00110011 00110011 00100000 00110100 01100011 00100000 00110100 00110100 00100000 00110110 00110001 00100000 00110100 00111000 00100000 00110011 00111000 00100000 00110111 00110111 00100000 00110011 00111001 00100000 00110011 00110110 00100000 00110111 00111000 00100000 00110110 00111001 00100000 00110110 01100001 00100000 00110100 00110101 00100000 00110100 01100101 00100000 00110110 00111001 00100000 00110110 00111001 00100000 00110011 00110011 00100000 00110111 00110111 00100000 00110011 00111000 00100000 00110100 00110100 00100000 00110111 00111000 00100000 00110101 00110111 00100000 00110100 00110011 00100000 00110100 00110011 00100000 00110111 01100001 00100000 00110100 00110111 00100000 00110110 00110111 00100000 00110011 00110111 00100000 00110011 00110010 00100000 00110110 00110101 00100000 00110110 00110010 00100000 00110011 00110100 00100000 00110100 01100110 00100000 00110011 00110110 00100000 00110011 00110010 00100000 00110111 00110111 00100000 00110111 00110110 00100000 00110100 00110001 00100000 00110100 00110100 00100000 00110011 00110111 00100000 00110100 00111001 00100000 00110100 01100110 00100000 00110011 00110111 00100000 00110110 00110101 00100000 00110101 00110111 00100000 00110110 00111000 00100000 00110111 00111000 00100000 00110011 00111001 00100000 00110111 00111000 00100000 00110011 00110001 00100000 00110100 00110100 00100000 00110101 00110000 00100000 00110111 00110000
Once it’s decoded to ASCII, we get the following hex encoded text, hence we can use the previous tool again.
32 65 6e 54 64 30 55 42 4d 73 55 68 33 4c 44 61 48 38 77 39 36 78 69 6a 45 4e 69 69 33 77 38 44 78 57 43 43 7a 47 67 37 32 65 62 34 4f 36 32 77 76 41 44 37 49 4f 37 65 57 68 78 39 78 31 44 50 70
Now we get a base62 encoded text.
2enTd0UBMsUh3LDaH8w96xijENii3w8DxWCCzGg72eb4O62wvAD7IO7eWhx9x1DPp
After decoding it we get a base64 encoded text.
Y2liZXJnYWx7SGFzX2Rlc2NvZGlmaWNhZG9fbGFfZmxhZ30=
Finally we get our flag.
cibergal{Has_descodificado_la_flag}
RSA Madness
Alberto, el hermano pequeño de Alicia, ha creado dos claves RSA 1024 por miedo a extraviar una de ellas. Aunque su hermana se lo ha desaconsejado, a Alberto le ha parecido una gran idea que ambas claves compartan el mismo módulo (n), como se puede observar analizando sus respectivas claves públicas: pub_key1.pem y pub_key2.pem
Bernardo ha enviado un mensaje cifrado a Alberto, utilizando aes-256-cbc, con el vector de inicialización (IV) a 0, y ha cifrado la clave AES de 256 bits con la primera clave pública RSA de Alberto. En tu puesto de vigilancia has obtenido el mensaje cifrado con AES (flag.enc) y la clave AES cifrada (aes_key.enc1).
Como era previsible, Alberto ha extraviado la clave privada asociada a su primera clave RSA, por lo que solicita a Bernardo que le remita de nuevo la clave AES cifrada con su segunda clave pública RSA, información que también has obtenido (aes_key.enc2).
¿Serás capaz de descifrar la clave AES y acceder al mensaje cifrado?
For this challenge we are given 4 files:
pub_key1.pempub_key2.pemaes_key.enc1aes_key.enc2flag.enc
If we analyse the public key files, we can notice that both have the same modulus (n) but a different public exponent (e). They share the same modulus, and both aes_key.enc1 and aes_key.enc2 files come from the same plaintext message. Therefore, this can be solved with the common modulus attack.
Attack
In order to get the attack to work, both exponents must be coprimes, that is, $mcd(e_1, e_2)=1$. If so, that means that we have two numbers $x$ and $y$ such that: $$xe_1 + ye_2 = 1$$ To find $x$ and $y$ we use the Extended Euclidean algorithm. Once we find them, its easy to get the plaintext. Having $C_1=M^{e_1} \bmod n$ , and $C_2=M^{e_2} \bmod n$ :
$$ \begin{aligned} C^x_1 * C^y_2 &= (M^{e_1})^x * (M^{e_2})^y \newline &= M^{e_1x} * M^{e_2y} \newline &= M^{e_1x + e_2y} \newline &= M^1 \newline &= M \end{aligned} $$
Challenge Solution
We could write an script to solve this what we explained pre To solve this challenge we could translate what we explained to code. However, there’s already a github repository with a python script that fits perfectly with what we need. RSA-Common-Modulus-Attack.
To get the AES key used to encrypt the flag.enc file, we run the script:
# enc1 y enc2 son los ficheros de aes en base64
rsa-cm.py -c1 enc1 -c2 enc2 -k1 pub_key1.pem -k2 pub_key2.pem
And we get the following output.
[+] Recovered message:
30593212847270711399711376013419410780738043650221125144037099091540978173011
[+] Recovered bytes:
b'C\xa3%\x14\x9f\xb5C\xa2"tb\x9e\xf6\xbf\xd3l\xb0\xb6Lpg\x8c\nO\x02\xd7x\xb0\x14\xb4\x04S'
Now we can easily decrypt the flag.enc file with an online tool like Cryptii. We only need to hex encode the flag.enc file and the output obtained from the common modulus attack.
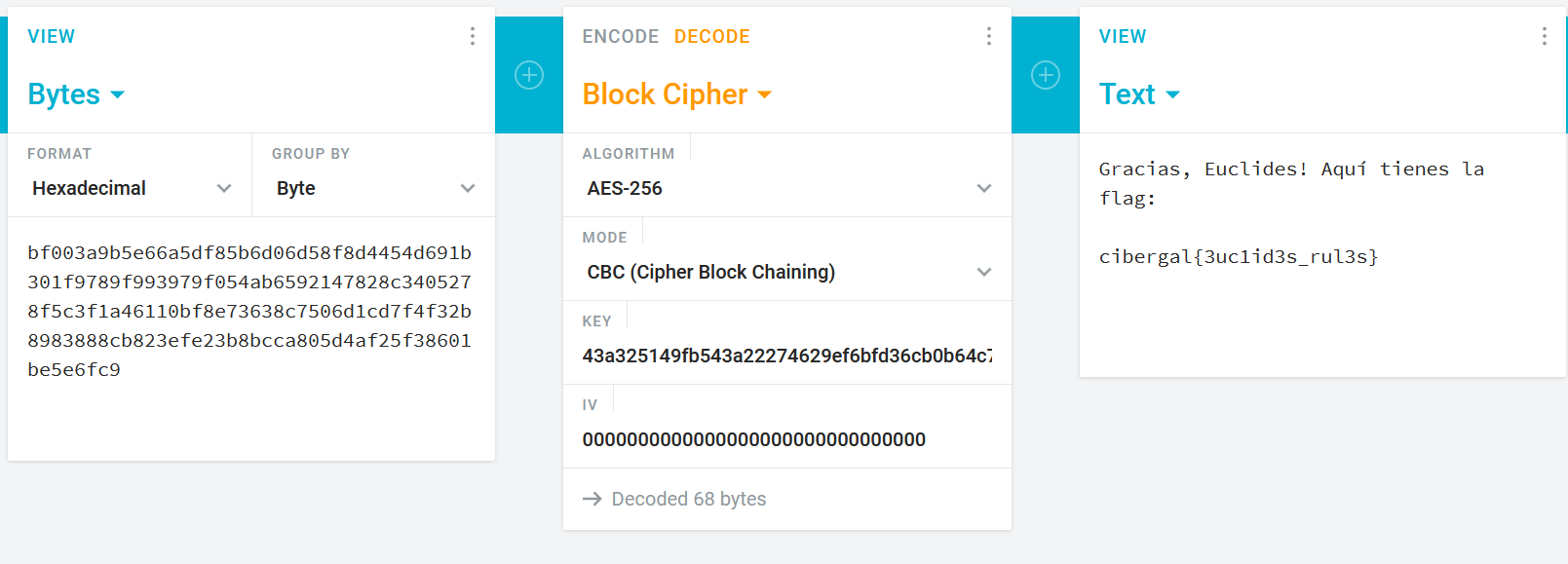
Flag:
cibergal{3uc1id3s_rul3s}
RSA Madness 2
De nuevo Alberto, el hermano pequeño de Alicia, ha creado un servicio web (https://cibergalctf-rsa-madness-2.chals.io) que devuelve firmado con su primera clave RSA el número que se proporcione. Desoyendo de nuevo los consejos de su hermana, ha utilizado esa clave para recibir información confidencial. Bernardo ha enviado a Alberto cifrado con la clave pública RSA (pub_key1.pem) un mensaje que has podido interceptar (flag2.enc)
On this challenge we are given 2 files
pub_key1.pemflag2.enc
And we are given an url from a signing web service. This webapp signs any number that we write as input. The private key used for signing is the one from the key pair used to encrypt the flag2.enc file.
Using the same key pair for signing and encripting files it’s a serious security issue. A bad actor could paste an encrypted message as input and get its plaintext version.
On the next table we can see the functions used for signing, encrypting and decrypting.
| Encrypting | Decrypting | Signing |
|---|---|---|
| $C=m^e \bmod n$ | $m=C^d \bmod n$ | $S=m^d \bmod n$ |
As you can see, if a message that has been enrypted with the public key is signed, the message would be decrypted.
However, when we try to send the encrypted message as an integer to the web application, we are given the following output.

It seems that the application doesn’t allow us to sign a message that has been previously encrypted with the public key associated to the private key used for signing.
That being the case, we should find a way of sending that encrypted message without the web service knowing that it is that message. In order to do this, we will use a method called blind signature.
Blind Signature
Blind signature is used when, for privacy and anonimity, an user wants to have a message signed without the signer knowing what the message is.
First, we choose a number $k$ that is coprime to $n$. Being $n$ the modulus and $e$ the public exponent, we blind the message like this.
$$m' \equiv mk^e \bmod n$$
Now, we send the blinded message $m'$ to be signed.
$$S' \equiv (m')^d \bmod n \equiv (m^ek^e)^d \bmod n$$
Finally, we divide the result by $k$ so that we get the unblinded message. Since $m'$ is equal to $k^{ed}$ , once we divide it by $k$, we’d have $1^{ed}$, that is $1$.
$$S = \frac{S'}{k} \bmod n$$
Solving the challenge
Now that we know how this method works, let’s try it out.
First, we should turn flag.enc into an integer. It has the following value:
m = 136303048756995810157940716185032667111830612010597107406495676976962913830094230393545978589443439249697298402573338272253640904169975859184422021013590534948130017584626517376422117912593883984359625006567897844040686762271735646197621493539236449652734497036337238540068933149508980465458044755934584078886
Next, we should get $e$ y $n$ from the pub_key1.pem file
e = 65537
n = 154087653999555555446998804473067505160067050493140267558659897792940250300855911633655658601345747714095446260307217652438694220001628702699560693661391270787633897136259675951607773082816805013014361131686525312985034121386722108595596708517831422886817991765720117085738934471183106649399960872754505418483
Now, we choose a number that is coprime to n. For instance 2
Next we blind our message. To do the math we can use ipython.
m1 = m*(k**e) % n
We send the result to the application and we get the following number.
s1 = 7849746955854748602350158963065991715871888549798095025878829707724270519846341645847019231536931761434479614627261827551978821373938357638164
Finally, to get our plaintext flag, we only have to divide this result by $k$ (k=2) and convert to bytes afterwards.
from Crypto.Util.number import long_to_bytes
k = 2
s1 = 7849746955854748602350158963065991715871888549798095025878829707724270519846341645847019231536931761434479614627261827551978821373938357638164
a = long_to_bytes(s1 // k)
print(a.decode('utf-8'))
Flag:
Resuelto usando firma ciega!!
cibergal{RSA_love_is_blind}